अन्तरिक्ष में जहाँ गुरुत्वाकर्षण नगण्य होता है वहाँ यदि दूध छलकता है तो वो गोलाकार आकृति धारण कर लेता है ताकि उसका क्षेत्रफल कम-से-कम हो सके। इसके कारण वह वहीं घूमता रहता है और नीचे भी नहीं आ पाता है। एक छोटा कीट गुरुत्व से भयमुक्त होकर हवा में छलांग लगा सकता है और बिना किसी परेशानी के छत पर भी चढ़ सकता है। अलबत्ता एक बल ऐसा है जो कीट के लिये उतना ही खतरनाक होता है जितना कि गुरुत्वाकर्षण बड़े प्राणियों के लिये होता है। यूँ तो विभिन्न आकार के प्राणियों की शारीरिक बनावट में कई अन्तर दिखते हैं परन्तु यदि कोई प्रत्यक्ष अन्तर दिखता है तो वह है उनके आकार में। फिर भी जाने क्यों प्राणिशास्त्री इस बात पर कम ही ध्यान देते हैं। प्राणिशास्त्र की कई किताबों में इस बात का कोई जिक्र नहीं मिलता कि क्यों चील पक्षी गोरैया चिड़िया से बड़ा होता है, या दरियाई घोड़ा किसी खरगोश से विशाल क्यों होता है? हालांकि कहीं-कहीं पर कुछ अस्पष्ट-सी तुलना चूहे और विशाल ह्वेल के आकार के बारे में की जाती है। परन्तु आपको यह जानकर शायद आश्चर्य होगा कि विज्ञान के सरल नियमों से यह दिखाना बहुत आसान है कि क्यों समुद्र में पाई जाने वाली हिलसा मछली एक दरियाई घोड़े के जितनी बड़ी नहीं हो सकती या एक ह्वेल, हिलसा मछली के जितनी छोटी नहीं हो सकती (हाथी एक ह्वेल के बराबर विशाल नहीं हो सकता या एक चींटी हाथी के आकार की नहीं हो सकती)। जानवर की हरेक बनावट के लिये एक सर्वाधिक स्थायी और सुविधाजनक आकार होता है। दूसरे शब्दों में, आकार में बड़ा अन्तर लाने के लिये बनावट में भी परिवर्तन लाना जरूरी हो जाता है। सामान्यतः बड़ी वस्तुएँ छोटी वस्तुओं से मेल नहीं खातीं। परन्तु ऐसा क्यों?
इस लेख में हम प्रकृति की अपार विविधताओं को विज्ञान के सरल नियमों से समझने की कोशिश करेंगे।
एक सरल मापांक जिसे हम अपने दैनिक जीवन में उपयोगी पाते हैं, वह है- BMI अर्थात Body Mass Index (शरीर द्रव्यमान सूचकांक)। BMI शरीर में द्रव्यमान और ऊँचाई के सन्तुलन को इंगित करता है। गणितीय रूप मे: BMI = द्रव्यमान (किग्रा)/लम्बाई2 (मीटर2)। एक स्वस्थ व्यक्ति का BMI 20-24 के मध्य होना चाहिए। उदाहरण के तौर पर यदि आपका वजन 70 किलोग्राम तथा लम्बाई 1.8 मीटर है तो आपका BMI लगभग 23 होगा जो कि स्वस्थ होने को इंगित करता है। 25 से अधिक BMI वालों को अपना वजन कम करने की आवश्यकता है तथा 20 से कम BMI वालों को अपने शरीर का वजन बढ़ाने की आवश्यकता है। हालांकि आज-कल कम BMI का प्रचलन बढ़ गया है। फैशन एवं फिल्म उद्योग में एक बहुत प्रचलित शब्द है- साइज जीरो। 18 BMI से कम वाले व्यक्ति को साइज जीरो शरीर वाला मानते हैं। चिकित्सीय रूप से तो वह व्यक्ति स्वस्थ नहीं माना जाएगा, पर ग्लैमर की दुनिया में वह खूबसूरती का एक पैमाना जरूर बन गया है। वर्तमान में भी इसके कई उदाहरण मौजूद हैं जैसे फिल्मी दुनिया को ही देख लीजिए। आपको कई अभिनेत्रियाँ साइज जीरो की दिख जाएँगी।
एक और सरल नियम जिससे प्रकृति की बहुत सारी विविधताओं को समझा जा सकता है वह है क्षेत्रफल-आयतन नियम। इसे संक्षेप में s/v (surface area/volume) भी कहते हैं। किसी आकार को छोटा या बड़ा करने पर उसके आयतन व क्षेत्रफल एक अनुपात में परिवर्तित नहीं होते। उदाहरणस्वरूप एक घनाकार वस्तु को लेते हैं जिसकी प्रत्येक भुजा की लम्बाई ‘a’ है। इसका क्षेत्रफल 6a2 तथा आयतन a3 हुआ। अब यदि घन की लम्बाई हर दिशा में दोगुनी कर दी जाये तो उसका क्षेत्रफल 24a2 तथा आयतन 8a3 हो जाएगा। हम देख सकते हैं कि आयतन में तो आठ गुना वृद्धि हुई जबकि क्षेत्रफल में केवल चार गुना। बड़े घन के लिये क्षेत्रफल-आयतन अनुपात छोटे घन की तुलना में आधा है। अतः जैसे-जैसे हम किसी वस्तु को छोटा करते जाएँगे उसके s/v अनुपात में वृद्धि होती जाएगी। सरल भाषा में कहें तो छोटी वस्तु का पृष्ठीय क्षेत्रफल उसी आकार की बड़ी वस्तु से तुलनात्मक रूप से अधिक होता है।
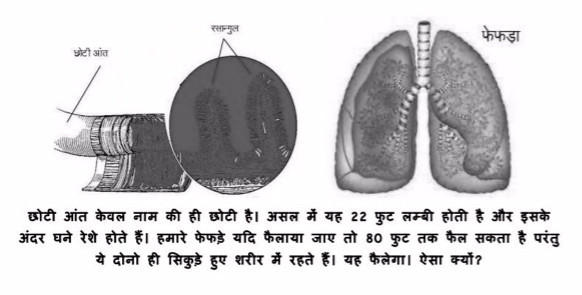
प्रकृति भी इस बात को बखूबी जानती है कि क्षेत्रफल अधिक या कम होने से क्या-क्या लाभ या हानि हो सकते हैं। पेड़ों को ही देख लीजिए। उनमें पत्तियाँ अधिक होती हैं जिससे उनका पृष्ठीय क्षेत्रफल बढ़ जाये और वह ज्यादा-से-ज्यादा प्रकाश संश्लेषण कर सकें। वहीं दूसरी ओर मरुस्थलीय क्षेत्रों में उगने वाले पौधे जैसे की कैक्टस इत्यादि अपने क्षेत्रफल को कम रखने का प्रयास करते हैं क्योंकि अधिक क्षेत्रफल होने से वाष्पीकरण भी अधिक होता है। उनके तने ही प्रकाश संश्लेषण का कार्य करते हैं। हमारे शरीर में फेफड़े इसका ही एक और उदाहरण है। फेफड़ों में त्वचा एक गुच्छे के रूप में रहती है जिससे उसका वास्तविक क्षेत्रफल सैकड़ों वर्गमीटर तक बढ़ जाता है। यदि एक वयस्क शरीर के फेफड़ों को किसी समतल पर फैलाया जाये तो वह एक टेनिस कोर्ट के बराबर होगा। जितना अधिक क्षेत्रफल उतना ही अधिक ऑक्सीजन के अवशोषण की क्षमता। इसी तरह आँत एक कुंडली के समान रहती है और उसके अन्दर की तरफ बहुत सी छोटी-छोटी नालियों के समान संरचनाएँ निकली रहती हैं, जिन्हें रसान्गुल कहते हैं। जिससे आँतों का पृष्ठीय क्षेत्रफल कई गुना तक बढ़ जाता है। इस तरह से हमारे शरीर में भोजन से पोषक तत्वों को अवशोषित करने की क्षमता बढ़ जाती है जैसे कि रेशेदार तौलिए के रोएँ हमारे शरीर से पानी सोखते हैं। एक मनुष्य की आँतों की लम्बाई उनकी शरीर की लम्बाई से 10 गुना अधिक होती है। दैनिक जीवन में भी इसका कम महत्त्व नहीं है। एक बाटी या लिट्टी को पकाने में जितना समय लगता है उससे कहीं बहुत कम समय उसी द्रव्यमान की चपाती को पकाने में लगता है। चपाती के चपटे गोल आकार के कारण इसकी ऊष्मा अवशोषण करने की क्षमता बढ़ जाती है और वह पूर्णतः जल्दी पक जाती है। गोबर से कंडे बनाते हुए उसका पृष्ठीय क्षेत्रफल बढ़ाने के लिये चपटा किया जाता है जिससे उसको धूप में जल्दी से सुखाया जा सके। सतह क्षेत्रफल ज्यादा होने से वस्तु ज्यादा अभिक्रियाशील भी हो जाती है क्योंकि अब क्रिया करने के लिये अधिक क्षेत्रफल उपलब्ध रहता है। इसीलिये आयुर्वेदिक दवाइयों को महीन पीसकर खिलाया जाता है। लकड़ी का एक बड़ा लट्ठा जहाँ रात भर जलता रहता है, वहीं दूसरी ओर यदि उसके खपच्चियाँ बनाकर जलाया जाये तो वे शीघ्र ही जल जाएँगी। ठंड में जानवर अपने आप को गोलाकार बनाकर झुण्ड में सोते हैं जिससे उनका क्षेत्रफल कम हो और ऊष्मा का क्षय भी कम हो। ये सभी क्षेत्रफल-आयतन अनुपात के उदाहरण हैं।
चलिए, अब मापन के दूसरे पैमाने की बात करते हैं। पौराणिक आख्यानों में वर्णित एक विशालकाय राक्षस का उदाहरण लेते हैं। मान लेते हैं कि वह करीब साठ फुट लम्बा है। यानी सामान्य मनुष्य से दस गुना ऊँचा है बल्कि दस गुना चौड़ा और दस गुना मोटा भी है। अतः ऐसे किसी राक्षस का आयतन सामान्य व्यक्ति की तुलना में हजार गुना हुआ। अब चूँकि द्रव्यमान = घनत्व X आयतन और यदि मान लिया जाये कि राक्षस का घनत्व परिवर्तित नहीं होता है तो इस गणना से राक्षस का द्रव्यमान भी हजार गुना हो जाएगा अर्थात 70-80 टन का होगा। दुर्भाग्यवश उनकी हड्डियों की अनुप्रस्थ काट अथवा क्षेत्रफल केवल 2 दिशाओं में अर्थात मात्र 100 गुना बढ़ेगा। यदि मनुष्य की जाँघ की हड्डियों के 1 वर्ग इंच क्षेत्रफल को 1 किलोग्राम वजन सहन करना है तो राक्षस की हड्डियों को 1000 किलोग्राम। परन्तु मानव हड्डियों की क्षमता केवल इतनी होती है कि वे दस गुने से ज्यादा वजन में टूट जाती हैं। तो ऐसे में राक्षस के एक कदम बढ़ाते ही उसकी जाँघ की हड्डी टूटना निश्चित है। शायद इसलिये कुम्भकर्ण जैसा विशालयकाय राक्षस हमेशा लेटा रहता था।
प्राचीन मन्दिरों के खम्भे भी बहुत चौड़े इसलिये होते थे क्योंकि उन्हें अपने ऊपर वजनी गुम्बद रखना पड़ता था। गाय या बैल का सिर भी सामान्य से बहुत बड़ा होता है इसलिये उसे उठाने के लिये चौड़ी गर्दन भी चाहिए और शायद इसलिये डायनासोर का सिर उसके विशालकाय शरीर की तुलना में छोटा होता था। प्राणिशास्त्र के सन्दर्भ में चिंकारा, जो कि लम्बे और पतले पैरों वाला सुन्दर जानवर है, यदि विशालकाय होना चाहे तो उसके पास दो विकल्प हैं : या तो वह गैंडे के समान अपने पैर मोटे और छोटे कर ले (पैरों का लम्बा होना कतई आवश्यक नहीं है) अथवा जिराफ के समान अपने शरीर को सिकोड़ ले और पैर तिरछे करके शरीर से बाहर निकाल ले जिससे की वह आराम से खड़ा हो सके। हम इन जन्तुओं का उदाहरण इसलिये दे रहे हैं क्योंकि ये भी चिंकारा के समान ही तेज धावक हैं।गुरुत्वाकर्षण विशालकाय प्राणियों जैसे की दैत्यों, हाथियों या डायनासोर के लिये तो एक समस्या है परन्तु चूहे या मक्खी जैसे छोटे कीट के लिये यह कोई समस्या नहीं खड़ी करती। खदानों में एक छोटी चुहिया 50 मीटर यानी कि 10 मंजिल से भी ज्यादा ऊँची इमारत से गिरने पर भी जिन्दा बच जाती है। थोड़े बड़े आकार का कोई प्राणी गिरने पर जरूर मर जाएगा और मनुष्यों के तो अस्थि पंजर ही अलग-अलग हो जाएँगे। एक घोड़े का हाल तो उससे भी बुरा हो सकता है। कहने का अर्थ यह है कि आकार जितना बढ़ता जाएगा, उसके बचने की सम्भावना उतनी कम होती जाएगी। जब कोई वस्तु नीचे गिरती है तो उस पर हवा का प्रतिरोधक बल तथा पृथ्वी का गुरुत्वाकर्षण बल कार्य करता है। प्रतिरोधक बल वस्तु के क्षेत्रफल के समानुपाती (L2) तथा गुरुत्वाकर्षण बल वस्तु के वजन (L3) के समानुपाती होता है। अब यदि वस्तु का आकार दस गुना कम कर दें तो उसका वजन तो हजार गुना कम हो जाएगा परन्तु प्रतिरोधक बल केवल सौ गुना। यह नीचे गिराने में सहायक बल से अपेक्षाकृत दस गुना ज्यादा है। अतः प्राणी जितना छोटा होगा उसके नीचे गिरने पर बचने की सम्भावना उतनी ही ज्यादा होगी।
अन्तरिक्ष में जहाँ गुरुत्वाकर्षण नगण्य होता है वहाँ यदि दूध छलकता है तो वो गोलाकार आकृति धारण कर लेता है ताकि उसका क्षेत्रफल कम-से-कम हो सके। इसके कारण वह वहीं घूमता रहता है और नीचे भी नहीं आ पाता है। एक छोटा कीट गुरुत्व से भयमुक्त होकर हवा में छलांग लगा सकता है और बिना किसी परेशानी के छत पर भी चढ़ सकता है। अलबत्ता एक बल ऐसा है जो कीट के लिये उतना ही खतरनाक होता है जितना कि गुरुत्वाकर्षण बड़े प्राणियों के लिये होता है। यह बल है- पृष्ठ तनाव। स्नान करने के बाद हमारे शरीर पर लगभग पानी की 1-2 मिमी मोटी पर्त होती है। इसका वजन लगभग आधा किलोग्राम होता है। हमारे कुल वजन की तुलना में यह नगण्य है। पर एक कीट के पानी में भीगने पर उसके शरीर पर उसके वजन से कई गुना अधिक पानी रहेगा। और यह तो हम सभी जानते हैं कि किसी कीट के किसी द्रव पदार्थ (पानी, चाशनी या घटपर्णी के अन्दर का द्रव) के पृष्ठ तनाव की पकड़ में आने के बाद बाहर निकलना काफी मुश्किल होता है। कबीर का एक दोहा इस विषय में प्रासंगिक है-माखी गुड़ में गड़ी रहे पंख रहे लपटाए, हाथ मले और सिर धुने लालच बुरी बलाए।।
एक कीट को पानी के पास जाने में वैसा ही खतरा है जैसा कि हमारे किसी ऊँचे पहाड़ पर चढ़ने से- एक पैर फिसला और बचने की सम्भावना बहुत कम। इसलिये एक कीट का पानी से दूर रहना ही बेहतर है। पानी पर चलने वाले कीट अपने आपको पानी से गीला नहीं होने देते और अपने लम्बे पैरों की सहायता से पानी की सतह के ऊपर से ही चलते हैं।
विशाल धरातलीय जानवरों की अपनी अलग परेशानियाँ हैं। उनके शरीर में कार्यरत अंग छोटे प्राणियों से भिन्न होते हैं। एक हाथी या जिराफ को एक मनुष्य की तुलना में खून को अपेक्षाकृत अधिक ऊँचाई पर ले जाना पड़ता है जिसके लिये उन्हें उच्च रक्तचाप और शक्तिशाली धमनियों की आवश्यकता होती है। वहीं छोटे जानवर जैसे कि केंचुआ या चींटी अपनी त्वचा से अपने शरीर के अन्दर ऑक्सीजन लेते हैं। यदि एक केंचुएँ को हर दिशा में दस गुना बड़ा कर दें तो उसका वजन 1000 गुना अधिक हो जाएगा। ऐसे में यदि उसके अपने शरीर की मांसपेशियों को इस्तेमाल करना है तो उसे 1000 गुना अधिक ऑक्सीजन और भोजन की आवश्यकता होगी। परन्तु उसका पृष्ठ क्षेत्रफल केवल 100 गुना बढ़ेगा। ऐसे में उसके त्वचा और आँतों के प्रति वर्ग क्षेत्रफल को क्रमशः दस गुना ऑक्सीजन और भोजन की आवश्यकता की पूर्ति कैसे होगी? इसकी पूर्ति के लिये सतह की अवशोषण क्षमता को किसी तरीके से बढ़ाना पड़ेगा। हमारे शरीर में फेफड़े इसी का एक उदाहरण है। जैसे कि ऊपर हमने फेफड़ों और आँतों का जिक्र किया था, उनका क्षेत्रफल इतना अधिक है जो कि उनके पोषण के लिये पर्याप्त है। इस तरह बड़े आकार के प्राणियों में अंग भी संरचनात्मक तौर पर जटिल होते जाते हैं। विशाल जानवर अपनी जटिलता के कारण विशाल नहीं होते हैं बल्कि वो इसलिये जटिल होते हैं क्योंकि वे विशाल होते हैं। शरीर रचना विज्ञान मूलतः अपने शरीर का क्षेत्रफल अपने आयतन की तुलना में अधिक-से-अधिक रखना ही है।अब आपको बड़े आकार के लाभ के बारे में भी बता देते हैं। सबसे स्पष्ट यदि कोई लाभ है तो वह है अपने शरीर को गर्म रखने की क्षमता। हाथी, घोड़े, मनुष्य इत्यादि स्तनपायी जानवर गर्म खून (warm blooded animals) वाले प्राणी हैं। दूसरे शब्दों में, हम सभी उपापचय के दौरान गर्मी पैदा करते हैं। उपापचय हमारे भोजन की मात्रा पर निर्भर करता है। जैसा कि बताया गया है कि वस्तु से ऊष्मा का क्षय उसके पृष्ठ क्षेत्रफल के समानुपाती होता है। चाहे एक छोटा चूहा हो या मनुष्य, सभी के प्रति इकाई क्षेत्रफल से एक समान ऊष्मा का क्षय होता है, जिसके कारण सभी को गर्म रहने के लिये भोजन की मात्रा उनके शरीर के क्षेत्रफल के समानुपाती होनी चाहिए ना कि वजन के। एक चूहा अपने वजन का लगभग एक चौथाई खाना प्रतिदिन खा जाता है जो कि मुख्यतः उसके शरीर को गर्म रखने में प्रयुक्त होता है। वहीं मनुष्य आहार में रोज औसतन अपने वजन का 50वाँ हिस्सा लेता है। जैसे-जैसे गर्म खून वाले प्राणी का आकार छोटा होता जाता है, उनका पृष्ठीय क्षेत्रफल आनुपातिक रूप में बढ़ता जाता है और इसीलिये उनके खाने की मात्रा भी। उदाहरण के लिये सबसे छोटे पक्षी शकरखोरा (Humming bird) को अपने शरीर को गर्म रखने के लिये हर 4 घंटे में कुछ खाना पड़ता है। उसका भोजन भी पराग कण होता है जो कि बहुत समृद्ध आहार है। ठंडे प्रदेशों में न तो सरीसृप प्राणी (जिनमें अपने शरीर को गर्म रखने की क्षमता नहीं होती) पाये जाते हैं, न ही बहुत छोटे आकार के स्तनपायी। सबसे छोटा स्तनपायी जानवर जो कि आर्कटिक पर पाया जाता है वह है ध्रुवीय लोमड़ी। बहुत छोटे जानवर अपने शरीर को गर्म रखने के लिये पर्याप्त मात्रा में खा भी नहीं पाएँगे।
इस लेख में हमने मापन के कुछ नियमों की चर्चा की जिनके जरिए आप प्रकृति में उपयुक्त कई वस्तुओं को आसानी से समझ पाएँगे। लेकिन हम यह कतई नहीं कहना चाहते हैं कि प्रकृति की विराट विविधता को मापन नियमों में बाँध पाएँगे। हम यह मानते हैं कि यदि इन नियमों को समझ न भी पाएँ तो भी मायूस न होइए और प्रकृति की असीम सुन्दरता का आनन्द लीजिए।होमी भाभा विज्ञान शिक्षा केन्द्र
टाटा मूलभूत अनुसन्धान संस्थान
वी.एन. पुरव मार्ग, मानखुर्द
मुम्बई-400088
ई-मेल : vsingh@hbcse.tifr.res.in
Path Alias
/articles/parakartai-kae-maapana-naiyama
Post By: Editorial Team