
सारांश
जलविद्युत परियोजनाओं सहित विभिन्न प्रकार की जल संसाधन योजनाओं के नियोजन, विकास और संचालन के लिए अमापित और मापित आवाह क्षेत्र के लिए विभिन्न वापसी अवधि की बाढ़ के पूर्वानुमान के लिये उन्नत कार्यप्रणाली के अनुप्रयोग का बहुत अधिक महत्व है। इस प्रयोजन के लिए, एल-मोमेंट्स आधारित क्षेत्रीय बाढ़ आवृत्ति दृष्टिकोण बहुत अधिक प्रभावी हैं, क्योंकि ये प्रदर्शन के आधार पर अन्य दृष्टिकोण से बेहतर हैं। इस पत्र में, उप-हिमालयी क्षेत्र के 11 नदी प्रवाह मापक स्थलों के वार्षिक अधिकतम शिखर प्रवाह आंकड़ों का डिसकोरर्डेंसी माप (Di) का उपयोग कर जाँच की गयी और इस क्षेत्र की समरूपता के परीक्षण के लिये विषमता उपायों (H) का अनुप्रयोग किया गया है। रोबस्ट आवृत्ति वितरण की पहचान एल-मोमेंट्स अनुपात आरेख के आधार पर की गई है। मापित आवाह क्षेत्र के लिए विभिन्न वापसी अवधि की बाढ़ के पूर्वानुमान के लिए, रोबस्ट आवृत्ति वितरण के आधार पर एक क्षेत्रीय बाढ़ आवृत्ति संबंध विकसित किया गया है। अमापित आवाह क्षेत्र के लिये, विकसित संबंध को माध्यवार्षिक शिखरबाढ़ और जलग्रहण क्षेत्र के बीच एक क्षेत्रीय संबंध के साथ युग्मित किया गया है।
Abstract
For planning, development and operation of different types of water resources schemes including the hydropower projects, applications of new and advanced methodologies of prediction of floods of various return periods for ungauged, poorly gauged and gauged catchments is of great importance. For this purpose, L-moments based regional flood frequency approaches hold great potential as these are demonstrably superior to the other approaches. In this paper, annual maximum peak flow data of 11 streamflow gauging sites of the Sub-Himalayan region are screened using the Discordancy measure (Di) and homogeneity of the region is tested employing the heterogeneity measure (H). A robust frequency distribution is identified based on the L-moment ratio diagram. For the prediction of floods of various return periods for gauged catchments, a regional flood frequency relationship is developed based on the robust frequency distribution. For ungauged catchments, the developed relationship is coupled with a regional relationship between mean annual peak flood and catchment area.
1.0 परिचय
लघु, मध्यम और बड़ी पनबिजली परियोजनाओं का विकास बिजली उत्पादन के लिए सबसे अधिक आशाजनक और व्यवहार्य विकल्प में से एक है, चूंकि जल विद्युत उत्पादन पानी का गैर-उपभोगकारी उपयोग है और इस तरह की योजनाएं पर्यावरण के अनुकूल हैं और इसलिए, पर्यावरण संबंधी चिंताओं को कम से कम आकर्षित करती हैं। इसके अलावा, बिजली उत्पादन के लिए पानी एकमात्र निवेश है, जो एक अक्षय संसाधन है। हाइड्रोपावर परियोजनाएं हिमालय के पर्वतीय क्षेत्रों में बिजली उत्पादन के लिए आर्थिक रूप से सबसे अधिक व्यवहार्य हैं। सौभाग्य से, भारत जलविद्युत उत्पादन की विशाल क्षमता से संपन्न है और इसका केवल एक महत्वपूर्ण हिस्सा अभी तक उपयोग किया गया है। भारत की जल विद्युत क्षमता का अनुमान 60 प्रतिशत लोड फैक्टर पर 84,044 मेगावाट है। स्वतंत्रता (1947) के समय, जलविद्युत परियोजनाओं की स्थापित क्षमता 508 मेगावाट थी। 1998 के अंत तक स्थापित जल विद्युत क्षमता लगभग 22000 मेगावाट (88543 मेगावाट की कुल स्थापित क्षमता का 24.85 प्रतिशत) थी। एक अनुमान के अनुसार, भारत की बारवीं पंचवर्षीय योजना से 60,000 मेगावाट अतिरिक्त जल विद्युत का विकास करने की योजना है। इसमें दसवीं पंचवर्षीय योजना (2002-2007) के दौरान 14,393 मेगावाट, ग्यारहवीं (2007-2012) के दौरान 20,000 मेगावाट और बारहवीं (2012-2017) पंचवर्षीय योजनाओं के दौरान 26,000 मेगावाट शामिल हैं। इसके अलावा, देश के हिमालयी और उप-हिमालयी क्षेत्रों में लघु जल विद्युत परियोजनाओं के विकास से लगभग 10,000 मेगावाट की क्षमता उपलब्ध है। इसलिए, यह न केवल वांछनीय है, बल्कि इन क्षेत्रों में बिजली उत्पादन के लिए लघु, मध्यम और बड़ी पनबिजली योजनाओं के विकास के लिए एक मास्टर प्लान तैयार करने की आवश्यकता है।
भारतीय हाइड्रोलोजिक डिजाइन मानदंड़ों के अनुसार आवृत्ति आधारित बाढ़ विश्लेषण लगभग सभी प्रकार की हाइड्रोलिक संरचनाओं जैसे कि छोटे आकार के बांध, बैराज, वियर, सड़क और रेलवे पुल, जल निकासी संरचना, बाढ़ नियंत्रण संरचना आदि (बड़े और मध्यवर्ती आकार के बांधों को छोड़कर) के लिए डिजाइन बाढ़ के आकलन में सहायक हैं। हालांकि, बड़े और मध्यवर्ती आकार के बांधों के डिजाइन के लिए संभावित अधिकतम बाढ़ (पीएमएफ) और मानक परियोजना बाढ़ (एसपीएफ) को क्रमशः अनुप्रयोग किया जाता है (1)। इस प्रकार, जलविद्युत परियोजनाओं सहित छोटे आकार की जल संसाधन परियोजनाओं की य¨जना, विकास और संचालन के लिए, क्षेत्रीय बाढ़ आवृत्ति की नई और उन्नत तकनीकों का अनुप्रयोग आवश्यक हैं।
निम्न द्वारा कुछ बाढ़ आवृत्ति विश्लेषण अध्ययन किये गये हैंः (1) लैंडवेहर एट आल (2) होस्किंग और वालिस (3) होस्किंग और वालिस (4) जिन और स्टिंडजर (5) पॉटर और लेटनमैयर (6) फुर्काहर्सन (7) लेक¨बेलिस और फियोरेन्टीनो (8) मार्टिंस और स्टिंडजर (9) पील एट आल (10) क्लैप्स एवं लायो (11) जिंगी और हॉल। भारत में किए गए अध्ययनों में केंद्रीय जल आयोग (सीडब्ल्यूसी), अनुसंधान डिजाइन और मानक संगठन (आरडीएसओ) और भारत मौसम विज्ञान विभाग (आईएमडी) द्वारा संयुक्त रूप से किए गए अध्ययन शामिल हैं, जो भौगोलिक और मौसम संबंधी विशेषताओं पर विचार करते हुए कत्रिम यूनिट हाइड्रोग्राफ और डिजाइन वर्षा पर आधारित विधि का उपयोग करते हैं। संयुक्त राज्य अमेरिका भू-वैज्ञानिक सर्वेक्षण (यूएसजीएस) की कार्यविधि और पूल्ड वक्र तरीकों का उपयोग करके आरडीएसओ द्वारा क्षेत्रीय बाढ़ आवृत्ति अध्ययन किये गये। भारत के कुछ क्षेत्रों के लिए कुछ अनुसंधान और शैक्षणिक संस्थानों द्वारा एल-मोमेंट्स उपागम का उपयोग करके क्षेत्रीय बाढ़ आवृत्ति विश्लेषण अध्ययन किये गये हैं। वर्तमान अध्ययन में, भारत के उप-हिमालयी क्षेत्र उप जोन 7 के मापित एवं अमापित जलग्रहणों के लिए विभिन्न वापसी अवधियों की बाढ़ के आकलन के लिए एल-मोमेंट्स उपागम के आधार पर क्षेत्रीय बाढ़ आवृत्ति संबंध विकसित किए गए हैं।
2.0 एल-मोमेंट्स उपागम
एल-मोमेंट्स सांख्यिकी के भीतर एक नवीन विकास है। हाइड्रोलोजिकल अनुप्रयोगों की एक विस्तृत अनुप्रयोगों में एल-मोमेंट्स हाइड्रोलोजिक डेटा की विशेषताओं और वितरण के मापदंड़ों के सरल और उचित रूप से कुशल अनुमानक प्रदान करते हैं। एल-मोमेंट्स के तरीके उनके लिए बेहतर हैं जो पहले उपयोग किए गए हैं, और अब दुनिया भर में कई संगठनों द्वारा अपनाया जा रहा है Zafirakou-Koulouris एट आल उल्लेख करते है कि सामान्य उत्पाद मोमेंट्स की तरह, एल-मोमेंट्स सैद्धांतिक संभाव्यता वितरण और प्रेक्षित नमूनों की विशेषताओं या आकृतियों को संक्षेप में प्रस्तुत करते हैं। दोनों प्रकार के मोमेंट्स, वितरण स्थान (माध्य), स्केल (भिन्नता), तिरछापन (आकार) और कुर्टोसिस (शिखर) के उपाय प्रदान करते हैं। लेखकों ने आगे उल्लेख किया है कि एल-मोमेंट्स निम्न के कारण साधारण उत्पाद मोमेंट्स की अपेक्षा, विशेष रूप से पर्यावरणीय डेटा सेट के लिए महत्वपूर्ण लाभ प्रदान करते हैंः.
(क) एल-मोमेंट्स स्थान, पैमाने और आकार के अनुमानक लगभग निष्पक्ष होते हैं, भले ही संभाव्यता वितरण हो, जहां से अवलोकन उत्पन्न होते हैं (होस्किंग)।
(ख) एल-मोमेंट्स अनुपात के आकलनकर्ता जैसे कि एल-गुणांक भिन्नता, एल-स्केवनेस और एल-कुर्टोसिस पारंपरिक उत्पाद क्षण अनुपात की तुलना में, विशेष रूप से अत्यधिक तिरछे नमूनों के लिए कम पूर्वाग्रह प्रदर्शित कर सकते हैं।
(ग) L-भिन्नता के गुणांक और L-तिरछेपन के एल-मोमेंट्स अनुपात के अनुमानक की सीमा नहीं होती है, जो नमूना आकार पर निर्भर करती है, जबकि साधारण उत्पाद मोमेंट्स के अनुमानकों में होती हैं।
(घ) एल-मोमेंट्स आकलनकर्ता टिप्पणियों के रैखिक संयोजन होते हैं और इस प्रकार उत्पाद मोमेंट्स आकलनकर्ताओं की तुलना में नमूने में सबसे बड़ी टिप्पणियों के प्रति कम संवेदनशील होते हैं, जो प्रेक्षणों को वर्ग या घन करते हैं।
(च) एल-मोमेंट्स अनुपात आरेख अत्यधिक तिरछे डेटा के वितरण गुणों की पहचान करने में विशेष रूप से अच्छे हैं, जबकि साधारण उत्पाद मोमेंट्स आरेख इस कार्य के लिए लगभग बेकार हैं।
2.1 संभावना भारित मोमेंट्स और एल-मोमेंट्स
होस्किंग और वालिस ने बताया कि राज्य एल-मोमेंट्स सम्भाव्यता वितरण के आकार का वर्णन करने की एक वैकल्पिक प्रणाली है। ऐतिहासिक रूप से वे ग्रीनवुड एट आल के संभावित भारित मोमेंट्स (पीडब्लूएम) के संशोधनों के रूप में उत्पन्न हुए। संभाव्यता भारित मोमेंट्स को इस प्रकार परिभाषित किया गया हैः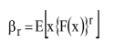 (1)
(1)
जिसको इस रूप में भी लिखा जा सकता है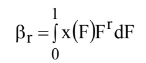 (2)
(2)
जहां F = F (x) x के लिए संचयी वितरण फंक्शन है, x (F) प्रायिकता पर मूल्यांकित x का व्युत्क्रम CDF है, और r = 0, 1, 2, ;, एक नाॅन नेगेटिक पूर्णांक है। जब r = 0, (0 वितरण के साधन μ = E 'x' के बराबर होता है किसी भी वितरण के लिए एल-मोमेंट्स का rth PWM के rth (होस्किंग, 1990) से संबंधित हैः
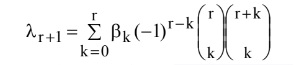 (3)
(3)
उदाहरण के लिए, पहले चार एल-मोमेंट्स का उपयोग कर PWM से संबंधित हैः
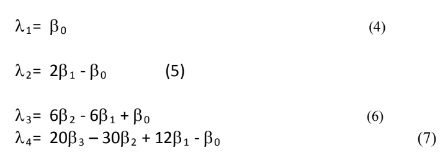
3.0 डिसकोरडेंसी परीक्षण का उपयोग करते हुए आंकड़ों की जांच
आंकड़ों की जांच का उद्देश्य यह जांचना है कि आंकड़े क्षेत्रीय बाढ़ आवृत्ति विश्लेषण करने के लिए उपयुक्त हैं। इस अध्ययन में आंकड़ों की स्क्रीनिंग L- मोमेंट्स आधारित डिसकोरडेंसी परीक्षण (Di) का उपयोग करके की गई थी। समूह में एन साइटें का विचार करके डिसकोरडेंसी परीक्षण (Di) क¨ परिभाषित किया गया है। T एक वेक्टर या मैट्रिक्स के ट्रांस्पोसिशन को दर्शाता है।
वर्गों और क्रॉस उत्पादों के योगों की मैट्रिक्स को इस प्रकार परिभाषित किया गया हैः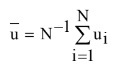 (11)
(11)
साइट i के लिए डिसकोरर्डेंसी को निम्न के रूप में परिभाषित किया गया हैः
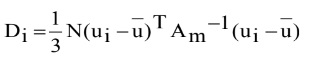 (13)
(13)
4.0 क्षेत्रीय समरूपता का परीक्षण
क्षेत्रीय समरूपता के परीक्षण के लिए, होस्किंग और वालिस ने एक सांख्यिकीय परीक्षण एच, जिसे विषमता उपाय के रूप में कहा जाता है, प्रस्तावित किया गया था। यह स्थनों के समूह के लिए नमूना एल-मोमेंट्स में स्थलों के बीच विविधताओं की तुलना करता है, जो एक सजातीय क्षेत्र से अपेक्षित होंगे। अंतर साइट भिन्नता के एल-मोमेंट्स अनुपात को मानक विचलन (वी) के रूप में मापा जाता है। यह निर्धारित करने के लिए कि एक सजातीय क्षेत्र से क्या अपेक्षा की जाएगी, अनुकार का उपयोग किया जाता है। चार पैरामीटर वितरण जैसे कि कप्पा वितरण का उपयोग करके क्षेत्रीय भारित औसत आंकड़ों के आधार पर बहुत सारे जैसे कि 500 आंकड़े क्षेत्र उत्पन्न किये जाते हैं। प्रत्येक उत्पन्न क्षेत्र की अंतर-साइट विविधता की गणना की जाती है और गणना की गई अंतर-साइट विविधता का माध्य ((μv) और मानक विचलन (σv) प्राप्त किया जाता है। फिर, विषमता माप H की गणना की जाती है।
 (14)
(14)
किसी क्षेत्र की विषमता का आकलन करने के लिए मानदंड हैंः यदि H < 1, इस क्षेत्र में एकरूप सजातीय हैय यदि 1 ≤ H < 2, क्षेत्र संभवतः विषम है; और यदि H ≥ 2 निश्चित रूप से क्षेत्र विषम है।
5.0 रोबस्ट क्षेत्रीय आवृत्ति वितरण का अभिनिर्धारण
एक सजातीय क्षेत्र के लिए एक उपयुक्त आवृत्ति वितरण का निर्माण क्षेत्रीय आंकड़ों के साथ औसत मोमेंट्स सांख्यिकी से वितरण की तुलना करके बनाया गया है। सबसे अच्छा फिट वितरण इस बात से निर्धारित ह¨ता है कि फिटेड वितरण के एल-स्कयूनेस और एल-कुर्टोसिस प्रेक्षित आंकड़ों के क्षेत्रीय औसत एल-स्कयूनेस और एल-कुर्टोसिस से मेल खाते हैं।
6.0 अध्ययन क्षेत्र और डेटा उपलब्धता
अध्ययन क्षेत्र में उप-हिमालयी क्षेत्र के छोटे और मध्यम आकार के जलग्रहण शामिल हैं। उत्तर-पूर्व में डेरा बाबा नानक के पास माधोपुर से गुजरने वाले महान चाप के भीतर स्थित हिमालय का क्षेत्र 760 से 960 ई देशांतर और 260 से 320 एन अक्षांशों को जोन-7 के अंतर्गत वर्गीकृत किया गया है। जो पूरे भारत जो विभाजित करने वाले 7 प्रमुख क्षेत्रों में से एक है। इन सात प्रमुख क्षेत्र को मध्यम आकार के 26 हाइड्रोलॉमेट्रोजिकल रूप से सजातीय उपजोन में विभाजित किया गया है। यह क्षेत्र पनबिजली उत्पादन के लिए एक बड़ी क्षमता रखता है लेकिन इस क्षेत्र के लिए बाढ़ का अनुमान एक अचूक समस्या साबित हो रहा है क्योंकि इस क्षेत्र से अपवाह में हिम गलन के साथ.साथ वर्षा भी होती है। इन दोनों महत्वपूर्ण प्रांचलों पर आंकड़ों की उपलब्धता अगर शून्य नहीं है तो पूरी तरह से अपर्याप्त है। इस अध्ययन के लिए डेटा उपलब्ध कराने वाली साइटों के जलग्रहण क्षेत्र 6 से 2,072 वर्ग किमी तक भिन्न ह¨ते हैं और उनकी औसत वार्षिक बाढ़ 17.1 से
1606.8 वर्ग किमी क ह¨ती है।
7.0 परिणामों का विश्लेषण
अध्ययन क्षेत्र के सभी 11 गेजिंग साइटों के लिए एल-मोमेंट्स के संदर्भ में डिसकोरडेंसी सांख्यिकी की गणना की गई है। यह देखा गया है कि सभी 11 साइटों के लिए Di मान 0.12 से 2.45 तक पाया गया है जो Di के महत्वपूर्ण मान 2,632 से कम है। इसलिए, डिसकोरडेंसी परीक्षण के अनुसार, क्षेत्रीय बाढ़ आवृत्ति विश्लेषण करने के लिए सभी 11 साइटों के डेटा का उपयोग किया जा सकता है।
7.1 क्षेत्रीय समरूपता का परीक्षण
अध्ययन क्षेत्र के लिए विषमता माप (एच) के मान की गणना की गई थी, जिसमें 11 गेजिंग साइटों के डेटा का उपयोग करने वाले कप्पा वितरण का उपयोग करके 500 सिमुलेशन किए गए थे। गणना में इसका मान 3,29 पाया गया। जैसा कि H का मान 1 से अधिक है। इसलिए, 11 प्रवाह गेजिंग साइटों से युक्त अध्ययन क्षेत्र, एक विषम क्षेत्र के रूप में पाया जाता है। फिर, सभी 11 साइटों के Di मानकों के आधार पर, उच्चतम Di यानी 2.45 वाली साइट को डेटा सेट से हटा दिया गया और 10 साइटों के डेटा का उपयोग करके विश्लेषण किया गया। इन 10 साइटों के डेटा सेट के लिए क्प का आँकड़ा 0.10 से 1.95 तक भिन्न पाया गया। चूंकि Di का मान 10 स्ट्रीम प्रवाह गेजिंग स्थलों वाले क्षेत्र के क्प के महत्वपूर्ण मान 2,491 से कम हैं। इसलिए, 10 साइटों का डेटा क्षेत्रीय बाढ़ आवृत्ति विश्लेषण के लिए उपयुक्त है। 10 साइटों के डेटा का उपयोग करते हुए, विषमता माप (एच) का मान 0.47 के रूप में गणना की गयी है। चूंकि यह मान (H) 1.0 से कम है, इसलिए अध्ययन क्षेत्र में 10 गेजिंग साइटें समरूप क्षेत्र बनाती हैं।
7.2 रोबस्ट क्षेत्रीय आवृत्ति वितरण की अभिनिर्धारण
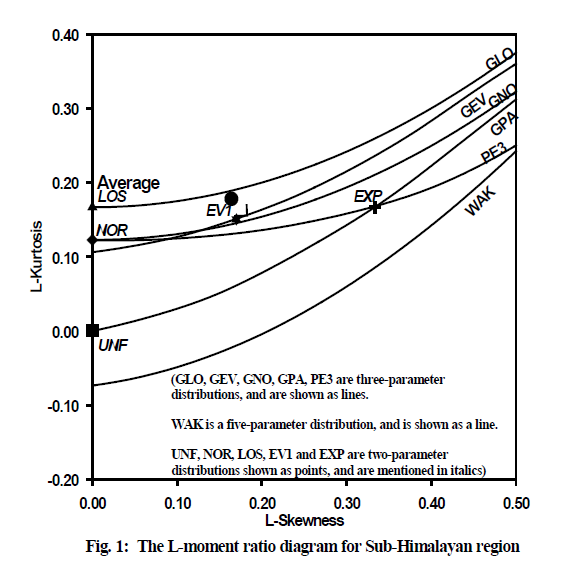
अध्ययन क्षेत्र के लिए रोबस्ट वितरण की पहचान करने के लिए एल-मोमेंट्स अनुपात आरेख का उपयोग सबसे अच्छा मानदंड के रूप में किया जाता है। L-skewness के क्षेत्रीय औसत मान अर्थात 0.3 = 0.1649 और L-kurtosis यानी 0.4 = 0.1770 प्राप्त होते हैं। चित्र 1 अध्ययन क्षेत्र के लिए एल-मोमेंट्स अनुपात आरेख दिखाता है। इस प्रकार, एल-मोमेंट्स अनुपात आरेख के आधार पर, जीएलओ वितरण को अध्ययन क्षेत्र के लिए रोबस्ट वितरण के रूप में पहचाना जाता है। जीएलओ वितरण के लिए क्षेत्रीय आवृत्ति संबंधों को नीचे व्यक्त किया गया है।
7.3 सामान्यीकृत लॉजिस्टिक वितरण (जीएलओ)
सामान्यीकृत लॉजिस्टिक वितरण (जीएलओ) का व्युत्क्रम रूप निम्नानुसार व्यक्त किया जाता हैः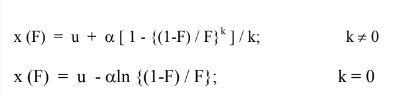 (15)
(15)
जहां u, α और k क्रमशः स्थान, पैमाने और आकार पैरामीटर हैं। लाॅजिस्टिक वितरण, सामान्यीकृत लाॅजिस्टिक वितरण का विशेष मामला है, जब k = 0 है।
7.4 मापित आवाह क्षेत्र के लिए क्षेत्रीय बाढ़ आवृत्ति सम्बन्ध
एल-मोमेंट्स अनुपात आरेख के आधार पर जीएलओ वितरण की अध्ययन क्षेत्र के लिए रोबस्ट वितरण के रूप में पहचाना की गयी है। इसलिए, इस वितरण का उपयोग करके क्षेत्रीय बाढ़ आवृत्ति संबंध विकसित किए गये हैं। अध्ययन क्षेत्र के मापित आवाह क्षेत्र के लिए जीएलओ वितरण के क्षेत्रीय प्राचालो के मान को प्रतिस्थापित करके क्षेत्रीय बाढ़ आवृत्तियों संबंधनों की व्युत्पत्ति की गयी जो निम्न प्रकार से हैः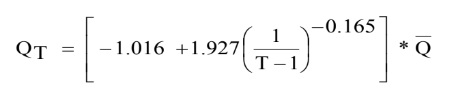 (17)
(17)
जहां, QT (m3/s), T वर्ष की वापसी अवधि के लिए बाढ़ है और जलग्रहण का वार्षिक शिखर बाढ़ (m3/s) है। अध्ययन क्षेत्र के छोटे से मध्यम आकार के जलग्रहण के लिए वांछित रिटर्न पीरियड की बाढ़ के आकलन के लिएए उपरोक्त क्षेत्रीय बाढ़ आवृत्ति संबंधों का उपयोग किया जा सकता है। वैकल्पिक रूप से, विभिन्न रिटर्न पीरियड्स की बाढ़ की गणना जीएलओ वितरण (तालिका 1 में दिए गए पर आधारित वृद्धि कारकों के संबंधित मूल्यों को जलग्रहण की औसत वार्षिक शिखर बाढ़ के साथ गुणा करके की जा सकती है।
तालिका 1ः उप-हिमाजयी क्षेत्र के लिए विभिन्न वितरणों के लिए वृद्धि कारकों () का मान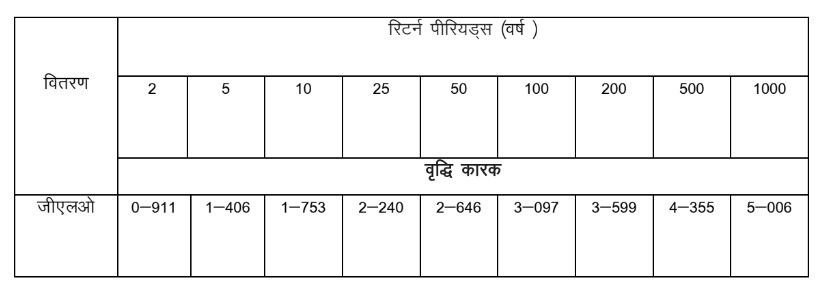 7.5 अमापित जलग्रहण के लिए क्षेत्रीय बाढ़ आवृत्ति संबंध
7.5 अमापित जलग्रहण के लिए क्षेत्रीय बाढ़ आवृत्ति संबंध
किसी स्थल पर टी वर्ष के रिटर्न पीरियड के बाढ़ के अनुमान के लिए, औसत वार्षिक शिखर बाढ़ के लिए अनुमान की आवश्यकता होती है। अमापित जलग्रहण कम किसी स्थल पर के लिए मनाया प्रवाह आंकड़ों की अनुपस्थिति में औसत की गणना नहीं की जा सकती है। ऐसी स्थिति में, औसत वार्षिक शिखर बाढ़ के आंकलन के लिए अमापित जलग्रहण की औसत वार्षिक शिखर बाढ़ और उसके प्रासंगिक शारीरिक और जलवायु विशेषताओं के बीच एक संबंध की आवश्यकता होती है। 10 मापित स्थलों के आंकड़ों के आधार पर लीस्ट वर्गों उपागम का उपयोग करके लॉग डोमेन में क्षेत्र के लिए क्षेत्रीय संबंध विकसित किये गये जो निम्न हैः.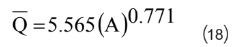 (18)
(18)
जहां, A वर्ग किमी में जलग्रहण क्षेत्र है, और ..... घन सेमी में औसत वार्षिक शिखर बाढ़ है। समीकरण (18) के लिए, निर्धारण का गुणांक, r2 = 0.74 है।
अमापित जलग्रहण के लिए विभिन्न रिटर्न अवधियों की बाढ़ के आकलन के लिए क्षेत्रीय बाढ़ आवृत्ति संबंध के विकास के लिए, समीकरण (17) में दिए गए क्षेत्रीय बाढ़ आवृत्ति संबंध को क्षेत्रीय वार्षिक बाढ़ और जलग्रहण क्षेत्र के बीच के क्षेत्रीय संबंधों के साथ युग्मित किया गया है, तथा समीकरण (18) में दिया गया है और निम्नलिखित क्षेत्रीय आवृत्ति संबंधों विकसित किया गया है। .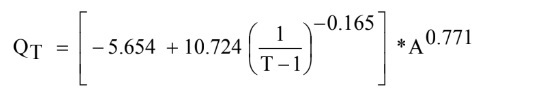 (19)
(19)
जहां, QT बाढ़ T वापसी अवधि के लिए घन समी में बाढ़ का आंकलन है, और A वर्ग किमी में जलग्रहण क्षेत्र है।
8.0 निष्कर्ष
इस अध्ययन के आधार पर निम्नलिखित निष्कर्ष निकाले गए हैंः-.
(क) उप-हिमालयी क्षेत्र के वार्षिक अधिकतम शिखर बाढ़ आंकड़ों का उपयोग कर डिसकोरडेंसी परीक्षण (Di) का अनुप्रयोग करते हुए किए गए आंकड़ों की स्क्रीनिंग की गयी। जो संकेत करते हैं कि सभी 11 मापन स्थलों के आंकड़े क्षेत्रीय बाढ़ आवृत्ति विश्लेषण के लिए उपयुक्त हैं। विषमता माप (H) के आधार पर अध्ययन क्षेत्र के 10 धारा प्रवाह मापन स्थलों के वार्षिक अधिकतम शिखर बाढ़ के आंकड़े एक सजातीय क्षेत्र का गठन करते हैं और क्षेत्रीय बाढ़ आवृत्ति विश्लेषण के लिए इसका उपयोग किया जाता है।
(ख) विभिन्न वितरण अर्थात EV1, GEV, LOS, GLO, UNF PE (3), NOR, GNO, EXP, GPA, KAP and WAK इत्यादि का अनुप्रयोग किया गया है। एल-मोमेंट्स का उपयोग कर वितरण के क्षेत्रीय प्राचलों का आंकलन किया गया गया है, एल-मोमेंट्स अनुपात आरेख के आधार पर, जी एल ओ वितरण के अध्ययन क्षेत्र के लिए रोबस्ट वितरण के रूप में अभिनिर्धारित किया गया है।
(ग) अध्ययन क्षेत्र के मापित आवाह क्षेत्र के लिए विभिन्न रिटर्न पीरियड्स की बाढ़ के आकलन के लिए जी एल ओ का उपयोग करते हुए या तो विकसित क्षेत्रीय बाढ़ आवृत्ति संबंधों का उपयोग किया जा सकता है अथवा आवाह क्षेत्र की औसत वार्षिक शिखर बाढ़ के वृद्धि कारकों के सापेक्ष मान के साथ गुणा किया जा सकता है।
(घ) अध्ययन क्षेत्र के अमापित जलग्रहण के लिए वांछित रिटर्न पीरियड की बाढ़ के आकलन के लिए, अमापित जलग्रहण के लिए विकसित क्षेत्रीय बाढ़ आवृत्ति संबंध का उपयोग किया जा सकता है।
(ङ) चूंकि क्षेत्र में 6 से 2,072 वर्ग किमी तक के जलग्रहण क्षेत्र के आंकड़ों का उपयोग करके क्षेत्रीय बाढ़ आवृत्ति संबंधों को विकसित किया गया है। इसलिए, इन संबंधों से अध्ययन क्षेत्र के जलग्रहण क्षेत्र के लिए विभिन्न रिटर्न अवधियों की बाढ़ के अनुमान प्रदान होने की उम्मीद है, जो क्षेत्र की सीमा के लगभग समान हवाई सीमा में हैं। इसके अलावा, औसत वार्षिक शिखर बाढ़ और जलग्रहण क्षेत्र के बीच संबंध 74 प्रतिशत प्रारंभिक विचरण (r2 = 0.74) की व्याख्या करने में सक्षम है। इसलिए अमापित जलग्रहण के मामले में अध्ययन के परिणाम इन सीमाओं के अधीन हैं। हालाँकि, अधिक सटीक बाढ़ आवृत्ति अनुमान प्राप्त करने के लिए क्षेत्रीय बाढ़ आवृत्ति संबंधों को परिष्कृत किया जा सकता है। जब कुछ अधिक मापन स्थलों के लिए आंकड़ें उपलब्ध हो जाते हैं और जलग्रहण क्षेत्र के अलावा अन्य भौतिक विशेषताओं के साथ साथ कुछ प्रासंगिक जलवायु विशेषताओं का भी उपयोग क्षेत्रीय बाढ़ आवृत्ति संबंधो के विकास के लिए किया गया है।
REFERENCES
- National Institute of Hydrology. Hydrologic design criteria, Course Material of Regional Course on Project Hydrology, Roorkee, 1992.
- Hosking, J.R.M. and Wallis, J.R., The value of historical data in flood frequency analysis, Water Resources. Research, 22 (11), 1606-1612, 1986.
- Hosking, J.R.M. and Wallis, J.R., The effect of intersite dependence on regional flood frequency analysis, Water Resources. Research, 24(4), 588-600, 1988.
- Jin, M. and Stedinger, J.R., Flood frequency analysis with regional and historical information’, Water Resources Research, 25(5), 925-936, 1989.
- Potter K.W. and Lettenmaier D.P., A comparison of regional flood frequency estimation methods using resampling method, Water Resources Research, 26, 415-424, 1990.
- Farquharson, J.R., Regional flood frequency analysis in arid and semi-arid areas, J. Hydrology, 138(3 & 4), 487-501, 1992.
- Kumar, R. C. Chatterjee and S. Kumar., Regional flood formulas using L-moments for small watersheds of Sone Subzone of India. J. Applied Engineering in Agriculture, American Society of Agricultural Engineers. Vol. 19, No. 1, pp.47-53, 2003.
- Kumar, R. and Chatterjee, C., Regional flood frequency analysis using L-moments for North Brahmaputra Region of India. Journal of Hydrologic Engineering, ASCE. Vol. 10, No. 1, 2005.
- Hosking, J. R. M. and Wallis, J. R., Regional frequency analysis-an approach based on L-moments, Cambridge University Press, New York, 1997.
- Zafirakou-Koulouris, A., Vogel, R. M., Craig, S.M. and Habermeier, J., L moment diagrams for censored observations, Water Resources Research, 34(5), 1241-1249, 1998.
/articles/ela-maomaentasa-kaa-upayaoga-karatae-haue-saba-haimaalayana-kasaetara-kae-laie-vaibhainana