
सारांश
वर्षा और वर्षा की तीव्रता के अनुमान, विश्लेषण और निर्धारण के ज्ञान का इंजीनियरिंग और कृषि विज्ञान में विशेष महत्व है। सिंचाई, जल निकासी और पानी के कटाव के नियंत्रण के लिए बांधों के आयाम, हाइड्रोलिंक परियोजनाओं के लिए और साथ ही नदी घाटियों की जलविज्ञान प्रक्रियाओं की समझ को सुविधाजनक करने के लिए यह नितांत आवशयक है। आमतौर पर हाइड्रोलिंक नियंत्रण संरचनाओं के डिजाइन और जल संसाधन इंजीनियरिंग परियोजनाओं की योजना और विकास के लिए वर्षा के तीव्रता-अवधि-आवृत्ति (आईडीएफ) वक्र का अनुमान आवश्यक होता है। सदैव आईडीएफ वक्र का उपयोग थोड़ा अधिक बोझिल हो जाता है और इसलिए अध्ययन क्षेत्र के लिए एक सामान्यीकृत अनुभवजन्य संबंध भी विकसित किया गया था। इस अध्ययन में दैनिक वर्षा आकंड़ों के सांख्यिकीय विश्लेषण के माध्यम से वर्षा की तीव्रता, अवधि और एक निश्चित वर्षा राशि की प्रत्यागमन अवधि के बीच संबंध निर्धारित किया गया है। उक्त अध्ययन तवी नदी बेसिन के लिए किया गया है, जो जम्मू और कश्मीर राज्य में स्थित है। इस अध्ययन हेतु वर्ष 1977 से 2007 के दैनिक वर्षा के आकंड़ों को भारतीय मौसम विभाग (IMD) से एकत्रित किया गया और IMD अनुभवजन्य कमी फाॅर्मूला का उपयोग करके कम अवधि की बारिश का आकलन किया गया और तत्पश्चात गमबेल की संभाव्यता वितरण पद्धति का उपयोग किया गया है। तवी नदी बेसिन में स्थित जम्मू, बटोट और भद्रवाह वर्षा स्टेशनों से एकत्र किए गए आकंड़ों का उपयोग 2, 5, 25, 50, 100, 200, 500 और 1000 वर्ष के प्रत्यागमन अवधियों के लिए 5, 10, 15 , 20, 25, 30, 35, 40, 45, 50, 60, 80, 100, 120 और 180 मिनट की अवधि के लिए वर्षा तीव्रता-अवधि-आवृत्ति वक्र को विकसित करने में किये गये हैं। इस अध्ययन द्वारा विकसित तीव्रता-अवधि-आवृत्ति (आईडीएफ) वक्र का उपयोग पुलिया, छोटे चेक डैम आदि की हड्रोलिंक डिजाइन एवं निर्माण में किया जाता सकता है।
मुख्य शब्दः तीव्रता-अवधि-आवृत्ति (आईडीएफ) वक्र, वर्षा की तीव्रता, प्रत्यागमन अवधि, अनुभवजन्य कमी सूत्र।
Abstract
Estimation of rainfall Intensity-Duration-Frequency (IDF) is commonly required for the design of hydraulic control structures and for water resources engineering planning and development. The use of IDF curves become more cumbersome and hence a generalized empirical relationship was also developed for the study area. The relationship between rainfall intensity, duration and the return period of a certain rainfall amount was determined through statistical analysis of rainfall data. Daily rainfall data for the year 1977 to 2007 were collected from Indian Meteorological Department (IMD) and the IMD empirical reduction formula was used to estimate the short duration rainfall using Gumbel’s probability distribution method. Rainfall data collected from the Jammu, Batote and Bhaderwah stations were used to develop the rainfall intensity duration frequency curves with return periods of 2, 5, 25, 50, 100, 200, 500 and 1000 years and using durations of 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 80, 100, 120 and 180 minutes. This study is an attempt to develop IDF curves, which are used in hydraulic design to size culverts and pipes.
Keywords: Intensity-Duration-Frequency (IDF) curve, Rainfall intensity, return period, IDF empirical reduction formula.
1.0 परिचय
जल जीवन का आधार है, और हमारी धरती पर वर्षा, शुद्ध जल का प्रारंभिक स्त्रोत है। सिंचाई, जल निकासी और मृदा के कटाव के नियंत्रण के लिए, बांधों के आयाम और हाइड्रोलिंक परियोजनाओं के लिए एवं कृषि योजना के प्रभावी नियोजन एवं क्रियान्वयन के लिए अति-वृष्टि (वर्षा) के गुणधर्मों पर ज्ञान अत्यधिक आवश्यक है। साथ ही साथ इसकी जानकारी नदी घाटियों की जलविज्ञानीय प्रक्रियाओं की समझ को बेहतर बनाती है। अपर्याप्त आकंड़ों के अभाव में की गई जल निकासी प्रणाली की आधी-अधूरी डिजाइन से जल भराव की समस्या होती है। जल निकासी प्रणाली के उचित डिजाइन के लिए कम अवधि की वर्षा की तीव्रता सबसे महत्वपूर्ण है (Rashid et al, 2012)। इसलिए, विभिन्न वापसी (प्रत्यागमन) की अवधि के लिए, वर्षा की आवृत्ति और तीव्रता मात्रा की विशेषता को जानना वांछनीय है। इसलिए, जल संसाधन इंजीनियरिंग में सबसे महत्वपूर्ण उपकरणों में से एक वर्षा की तीव्रता-अवधि-आवृत्ति (IDF) वक्र का प्रादुर्भाव हुआ, जो अत्यंत सरल किन्तु प्रभावी उपकरण के रूप मे काम कर सकता है। इसके माध्यम से जल संसाधन संरचना के जोखिम और भेद्यता का आकलन किया जा सकता है। साथ ही जल परियोजनाओं की योजना, डिजाइन और संचालन के लिए भी यह उपयोगी है। तीव्रता-अवधि-आवृत्ति (IDF) वक्र एक निश्चित समयावधि में वर्षा की तीव्रता का चित्रण करता है। दूसरे शब्दों में, आईडीएफ वक्र प्रत्येक वापसी अवधि के लिए समय अवधि (x अक्ष) के साथ वर्षा तीव्रता (y अक्ष) में प्लाॅट किया गया एक ग्राफ है। किसी स्थान या क्षेत्र के लिए IDF वक्र का विकास निम्न कारणों से इंजीनियरिंग अनुप्रयोग के लिए बहुत महत्वपूर्ण हैः 1) यह भविष्यवाणी करने में मदद करता है कि किसी स्थान या क्षेत्र में बाढ़ आएगी या नहीं। 2) यह इंगित करने में मदद करता है भविष्य में किसी स्थान या क्षेत्र में एक निश्चित वर्षा दर या अप्रवाह की एक विशिष्ट मात्रा की पुनरावृत्ति होगी या नहीं। 3) यह बाढ़ नियंत्रण संरचना के लिए डिजाइन निर्वहन के आकलन में मदद करता है। IDF वक्र से प्राप्त जानकारी का उपयोग तब हाइड्रोलिंक डिजाइन में पुलिया और पाइप के आकार को सुनिश्चित करने के लिए किया जाता है।
आईडीएफ वक्र संबंधो का विकास 1930 के दशक (Chow, 1988) से प्रारम्भ हुआ था। तब से दुनिया के कई क्षेत्रों के लिए इन संबंधो के विभिन्न रूपों का निर्माण किया गया है। इन अध्ययनाॅन में वर्षा की तीव्रता-अवधि-आवृत्ति संबंधो से जलवायु परिवर्तन और उसके प्रभावों का अध्ययन (Singh et al. 2016), समान तीव्र वर्षा क्षेत्रों का अध्ययन (Paixao et al. 2015), सेनेगल देश के लिए तीव्रता-अवधि-आवृत्ति संबंधो का विकास (Sane et al. 2018), जलविज्ञानीय डिजाइन के लिए अगली पीढ़ी के आईडीएफ वक्र (Yan et al. 2018) और बदलते जलवायु परिवर्तन और कम वर्षा आकंडे वाले क्षेत्रों का अध्ययन (Liew, Raghavan and Liong 2014) आदि प्रमुख हैं। सुदूर संवेदन और उपग्रह डेटा की आधुनिक तकनीक के साथ,Awadallah et al- (2011) ने क्षेत्रीय विश्लेषण और उपग्रह डेटा का उपयोग करते हुए दुर्लभ डेटा क्षेत्रों में आईडीएफ वक्र विकसित करने के लिए एक अध्ययन किया। IDF वक्र विकसित करने के लिए TRMM उपग्रह डेटा के साथ उपलब्ध ग्राउंड स्टेशनों के आंकड़ों का संयुक्त उपयोग किया। उन्होंने 24 घंटे की वर्षा की तीव्रता और कम अवधि की तीव्रता के बीच अनुपात विकसित करने के लिए एक विधि का उपयोग किया और रियाद क्षेत्र में वर्षा की तीव्रता का अनुमान लगाने के लिए एक अनुभवजन्य सूत्र विकसित किया।
वर्तमान शोध कार्य में एक तीव्रता-अवधि-आवृत्ति अनुभवजन्य सूत्र विकसित करने का प्रयास किया गया है, जो किसी भी अवधि के लिए वर्षा की तीव्रता और न्यूनतम प्रयास के साथ किसी भी प्रत्यागमन अवधि का अनुमान लगाने के लिए आईडीएफ वक्र के निर्माण में आगे मार्गदर्शन करेगा। तवी नदी का बेसिन के तीन स्थानों के वर्ष 1977 से 2007 तक के दैनिक वर्षा के आंकड़ों को भारत सरकार के मौसम विभाग (IMD) से एकत्रित किया गया और Gumbel के एक्सट्रीम वैल्यू डिस्ट्रीब्यूशन का उपयोग करके कम अवधि की बारिश का अनुमान लगाने के लिए IMD अनुभवजन्य सूत्र का उपयोग किया गया। IDF वक्रों को 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 80, 80, 100, 120 और 180 मिनट की छोटी अवधि की वर्षा के लिए तथा 2, 5, 25, 50, 100, 200, 500 और 1000 वर्ष की प्रत्यागमन अवधि के लिए प्लाॅट किया गया। आईडीएफ वक्र का उपयोग थोड़ा सा मुश्किल और लंबा है और इसलिए एक सामान्यीकृत अनुभवजन्य संबंध विकसित किया गया है। यह अध्ययन निम्नलिखित उद्देश्यों के साथ किया गया थाः
- दैनिक वर्षा के आंकड़ों से दैनिक अधिकतम वर्षा का अनुमान लगाना।
- विभिन्न वापसी अवधि के लिए तवी नदी के लिए आईडीएफ वक्र विकसित करना।
2.0 अध्ययन क्षेत्र
तवी नदी का बेसिन पश्चिमी हिमालय का एक छोटा सा हिस्सा है ज¨ 32 0-35 ‘से 33 0-35’ उतरी अक्षांश और 75 0 45 ‘से 75 0 45’ पूर्वी देशांतर के बीच स्थित है। इसके ऊपरी भाग में बेसिन संकरा और लम्बा है जबकि यह निचले हिस्से के साथ चैड़ा है। बेसिन के ऊपरी हिस्से में बीहड़ पहाड़ी स्थलाकृति की विशेषता है, जबकि निचले बेसिन में कम पहाड़ियों और एक क्रमिक मैदान है। बेसिन की ऊँचाई समुद्र तल से 400 मीटर से लेकर 4000 मीटर से तक विस्तारित है। बेसिन की औसत ऊंचाई समुद्र तल से लगभग 2200 मीटर ऊपर है। ऊपरी भाग में बेसिन की ढलान पूर्व से पश्चिम की और है, जबकि निचले हिस्से में उत्तर-पूर्व से दक्षिण के और इसके ऊपरी हिस्से में स्थित काली कुंडी ग्लैशियर की बर्फ के पिघलने से और इसके मूल में बारिश से तवी नदी में जल प्रवाह बारह माह रहता है। निचले जलग्रहण क्षेत्र में मुख्य रूप से बारिश होती है। तवी बेसिन का एक छोटा क्षेत्र (लगभग 200 वर्ग मीटर) बर्फ बाध्य है।
तवी नदी बेसिन ज्यादातर जम्मू, उधमपुर जिलों और डोडा जिलों के छोटे हिस्से के भीतर आती है। वर्तमान अध्ययन में, लगभग 1885 वर्गमीटर क्षेत्र जम्मू तक माना गया है। तवी बेसिन में जुलाई और अगस्त आम तौर पर लगभग 55 प्रतिशत बारिश के साथ सबसे खराब महीने होते हैं और नवंबर में कम से कम बारिश होती है और कुल बारिश का 2-3 प्रतिशत हिस्सा होता है। तवी जुलाई और अगस्त में भारी बाढ़ का अनुभव करती है। मानसून पहली जुलाई से भारी गरज के साथ शुरू होता है और सितंबर के मध्य तक चलता है। सामान्य वार्षिक वर्षा की अलग-अलग विशेषता है, तीन अलग सुविधाओं के साथः-
उत्तर पूर्वी जलग्रहण क्षेत्र में शामिल भद्रवाह और आसपास के क्षेत्र में, जहां जलवायु अतिरिक्त उष्णकटिबंधीय पहाड़ प्रकार है। पर्वत की जलवायु में भूमि की विशेषताओं के स्थान और दिशा के आधार पर तापमान और वर्षा में व्यापक भिन्नता है। इस क्षेत्र में सर्दी बहुत गंभीर है और दक्षिण-पश्चिम मानसून का प्रभाव नगण्य है। तवी नदी अपने मूल फर्म काली कुंडी ग्लेशियर पर बर्फ से ढकी है। काली कुंडी और सेओज-धार नवंबर में बर्फबारी का सामना करते हैं। हिमपात बहुत गहरा है और कुछ वर्षों में मई तक जारी रहता है।
मध्य क्षेत्र, जिसमे पूरा उधमपुर जिला और से युक्त है जहाँ जलवायु भी पहाड़ी प्रकार की है, लेकिन मानसून का पर्याप्त प्रभाव है।
दक्षिण-पश्चिमी क्षेत्र, जो मुख्य रूप से जम्मू जिले में आता है, जहाँ मानसून के प्रभाव से जलवायु गर्म होती है, क¨ वर्ष के कुछ भाग के दौरान उष्णकटिबंधीय आद्र्र और शुष्क जलवायु के समान कहा जा सकता है।
3.0 कार्य विधि
अध्ययन के उद्देश्यों को प्राप्त करने के लिए, वर्तमान अध्ययन में अपनाए गए डेटा और कार्यविधि को निम्नानुसार वर्णित किया गया हैः-
3.1 डेटा
इस अध्ययन में तवी नदी के जल प्रवाह क्षेत्र में स्थित तीन स्थानों जम्मू, भद्रावाह और बटोत के लिए वर्ष 1977 से 2007 तक के दैनिक वर्षा का डेटा भारत मौसम विज्ञान विभाग (IMD), पुणे से एकत्र किया गया था और प्रत्येक वर्ष के लिए अधिकतम 24-घंटे की वर्षा का डेटा निकाला गया था। इस डेटा का उपयोग छोटी अवधि की वर्षा की तीव्रता की अवधि की आवृत्ति के परिकलन के लिए किया गया।
3.2 छोटी अवधि की वर्षा का परिगणन
छोटी अवधि की वर्षा का परिगणन के लिए, भारतीय मौसम विभाग (IMD) ने वार्षिक अधिकतम मानों से 5, 10, 15, 20, 25, 25, 35, 40, 45, 50, 80,100, 100, 120 और 180 मिनट की विभिन्न अवधि वाली वर्षा के आकलन के लिए उपयोग किए जाने वाले अनुभवजन्य सूत्र (क्रमांक 1) का उपयोग किया। Chowdhury et al. (2007) द्वारा भी इसी भारतीय मौसम विज्ञान विभाग (IMD) अनुभवजन्य कमी के सूत्र का उपयोग दैनिक वर्षा के आंकड़ों से कम अवधि की वर्षा का अनुमान लगाने के लिए किया गया था।
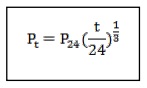
जहां, Pt = t- घंटा अवधिक में अपेक्षित वर्षा, मिमी
P24 = दैनिक वर्षा, मिमी
T = वर्षा की अवधि है जिसके वर्षा की मात्रा की आवश्यकता है, घंटे में
3.3 गमबेल की चरममान संभाव्यता वितरण प्रकार- पद्धति
विभिन्न प्रत्यागमन अवधियां के लिए अधिकतम वर्षा की तीव्रता का अनुमान विभिन्न संभावना का वितरण का उपयोग करके लगाया जाता है। गमबेल के संभाव्यता वितरण प्रकार-1 (चाउ एट अल, 1988) में चरम मानों के लिए सबसे अधिक व्यापक रूप से उपयोग होने वाले संभाव्य वितरण कायरों में से एक है। जिसका उपयोग अधिकतम बाढ़, अधिकतम हवा की गति, अधिकतम वर्षा आदि की भविष्यवाणी एवं निर्धारण के लिए जल विज्ञान और मौसम विज्ञान में बहुताते से होता है। इस शोध अध्ययन में गमबेल के चरम मान वितरण का उपयोग दैनिक वर्षा डेटा की संभाव्यता वितरण के लिए किया गया है।
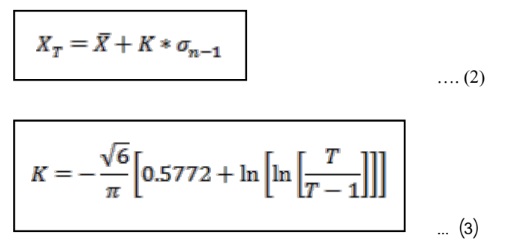
जहां, XT = प्रत्यागमन की अवधि, T के लिए यादृच्छिक वर्षा, मिमी
X = दैनिक औसत वर्षा, मिमी
σn-1 = वर्षा का उस अवधि में मानक विचलन, मिमी
K = आवृत्ति कारक जो प्रत्यागमन की अवधि, T और वितरण की आवृत्ति पर निर्भर करता है।
T = प्रत्यागमन की अवधि, वर्ष
3.4 विभिन्न अवधि पर वर्षा की तीव्रता की प्राप्ति
जम्मू, भद्रावाह और बटोट स्टेशनों के लिए तीव्रता-अवधि-आवृत्ति (IDF) वक्र विकसित करने में निम्नलिखित चरणों का उपयोग किया गया। 31 साल के वार्षिक अधिकतम वर्षा वाले डेटा का उपयोग करते हुये उनके औसत और मानक विचलन को परिगणित किया गया। सूत्र (2) के माध्यम से 5, 10, 15, 20, 25, 30, 35, 40, 45, 50. 60, 80, 100, 120 और 180 मिनट की अवधि के लिए वांछित वर्षा का आकलन किया गया। तत्पश्चात निम्न सूत्र द्वारा इस प्रत्यागमन की अवधियों के लिए वर्षा की तीव्रता की गणना की गई।
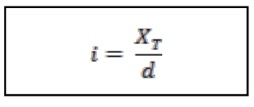 (4)
(4)
जहां, i = वर्षा की तीव्रता (मिमी/घंटा)
XT = किसी दिए गए प्रत्यागमन की अवधि (T) के लिए डिजाइन की गई वर्षा की मात्रा (मिमी)
d = वर्षा की अवधि (घंटे)
इस शोध अध्ययन में 2, 5 , 25, 50, 100, 200, 500 और 1000 वर्ष की प्रत्यागमन की अवधि के लिए आवृत्ति कारक को गमबेल के वितरण का उपयोग करके गणना की गई जैसा कि सूत्र (2) में अभिव्यक्त किया गया है ।
3.5 तीव्रता-अवधि-आवृत्ति अनुभवजन्य सूत्र
तीव्रता-अवधि-आवृत्ति (IDF) अनुभवजन्य सूत्र वह हैं जिससे विभिन्न अवधि की अधिकतम वर्षा की तीव्रता का अनुमान और विभिन्न प्रत्यागमन की अवधि के लिए लगाते हैं। अनेकों शोधकर्ताओं और वैज्ञानिकों द्वारा उक्त समब्म्ध में विभिन्न प्रक्रियाओं और सूत्रों का प्रस्ताव किया है (Chow, 1964; Bell, 1969; Chen, 1983; Aron et al. 1987; Kouthyari and Grade, 1992 )। तीव्रता-अवधि-आवृत्ति (IDF) दरअसल वर्षा की तीव्रता (i), उसकी अवधि (td) और प्रत्यागमन अवधि (T) के बीच एक गणितीय संबंध है। समीकरण (5) आईडीएफ अनुभवजन्य समीकरण का रूप है जो इस अध्ययन में उपयोग किया गया है।
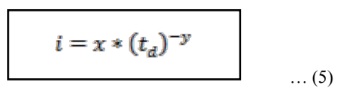
जहां, i = वर्षा की तीव्रता (मिमी/घंटा)
td = वर्षा की अवधि, मिनट
x और y = फिटिंग पैरामीटर
4.0 परिणाम और विवेचना
4.1 दैनिक अधिकतम वर्षा की परिगणना
वर्तमान अध्ययन में, 5, 10, 15, 20, 25, 30, 35, 40, 40, 45, 50, 60, 80, 100, 120 और 180 मिनट जैसे विभिन्न छोटी अवधि की वर्षा को वार्षिक अधिकतम 24 घंटे की बारिश के आंकड़ों से भारतीय मौसम विभाग के अनुभवजन्य सूत्र द्वारा अनुमानित किया गया है। जम्मू, बटोट और भद्रवाह स्टेशनों के इन परिणामों को क्रमश तालिकाओं क्रमांक 1, 2 और 3 में दिखाया गया है।
तालिका 1ः जम्मू स्टेशन के लिए दैनिक अधिकतम वर्षा
तालिका 2ः बटोट स्टेशन के लिए दैनिक अधिकतम वर्षा
तालिका 3ः भद्रवाह स्टेशन के लिए दैनिक अधिकतम वर्षा
4.2 विभिन्न प्रत्यागमन की अवधि के लिए वर्षा की तीव्रता
उपरोक्त अनुमानित छोटी अवधि के वर्षा डेटा का गमबेल के एक्सट्रीम वैल्यू टाइप.1 डिस्ट्रीब्यूशन (Chow et al. 1988) में उपयोग करके विभिन्न प्रत्यागमन अवधियों केडबल्यू लिए उनकी वर्षा की मात्रा को परिगणित किया गया और इसके परिणामों को तालिका क्रमांक 4, 5 और 6 में क्रमश जम्मू, बटोट और भद्रवाह स्टेशनों को दर्शाया गया है। जिसके द्वारा हमने तीव्रता-अवधि-आवृत्ति (आईडीएफ) वक्र का विकास किया।
तालिका 4ः जम्मू स्टेशन के लिए विभिन्न वापसी अवधियों के लिए वर्षा की तीव्रता
तालिका 5ः बटोट स्टेशन के लिए विभिन्न वापसी अवधियों के लिए वर्षा की तीव्रता
तालिका 6ः भद्रवाह स्टेशन के लिए विभिन्न वापसी अवधियों के लिए वर्षा की तीव्रता
जम्मू, बटोट और भद्रवाह स्टेशनों के लिए 5, 15, 30 और 60 मिनट की छोटी अवधि के लिए 100 वर्ष की वापसी अवधि के लिए अनुमानित वर्षा की तीव्रता की तुलना को तालिका 7 में प्रदर्शित किया गया है। नीचे दी गई तालिका 7 से यह निष्कर्ष निकाला गया कि बटोट में 5 मिनट की अवधि के लिए सर्वाधिकतम वर्षा की तीव्रता है।
तालिका 7ः विभिन्न स्टेशनों से प्राप्त आंकड़ों का उपयोग करके वर्षा की तीव्रता की गणना
| अवधि (मिनट) | जम्मू | बटोटे | भद्रवाह |
| 5 | 493.98 | 595.48 | 455.23 |
| 15 | 237.40 | 286.18 | 218.82 |
| 30 | 149.52 | 180.25 | 137.84 |
| 60 | 94.18 | 113.53 | 86.82 |
तालिका 8ः संबंधित रिटर्न अवधि के लिए अनुमानित आवृत्ति कारक
| वापसी की अवधि (टी वर्ष) | फ्रिक्वेंसी फैक्टर (K) |
| 2 | -0.16 |
| 3 | 0.25 |
| 5 | 0.72 |
| 10 | 1.30 |
| 25 | 2.04 |
| 50 | 2.59 |
| 100 | 3.14 |
| 200 | 3.68 |
| 500 | 4.39 |
| 1000 | 4.94 |
4.3 तीव्रता-अवधि-आवृत्ति (आईडीएफ) वक्र का विकास
IDF वक्र यानि वर्षा की तीव्रता-अवधि-आवृत्ति वक्र क 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 80, 100, 120 और 180 मिनट की छोटी अवधि के लिए विकसित किया गया और 2, 5, 25, 50, 100, 200, 500 और 1000 वर्ष की प्रत्यागमन अवधि के लिए विकसित किए गए जो चित्र क्रमांक 1, 2 और 3 में क्रमश जम्मू, बटोट और भद्रवाह स्टेशनों के लिए दर्शाये गए है। IDF वक्रों को देखने से पता चलता है कि अवधि बढ़ने के साथ बारिश की तीव्रता कम हो जाती है और प्रत्यागमन की अवधि में वृद्धि के रूप में विशेष अवधि के लिए वर्षा की तीव्रता बढ़ जाती है। चित्र 1, 2 और 3 क्रमशः जम्मू, बटोट और भद्रवाह स्टेशन के लिए वर्षा आईडीएफ घटता का प्रतिनिधि त्व करता है।
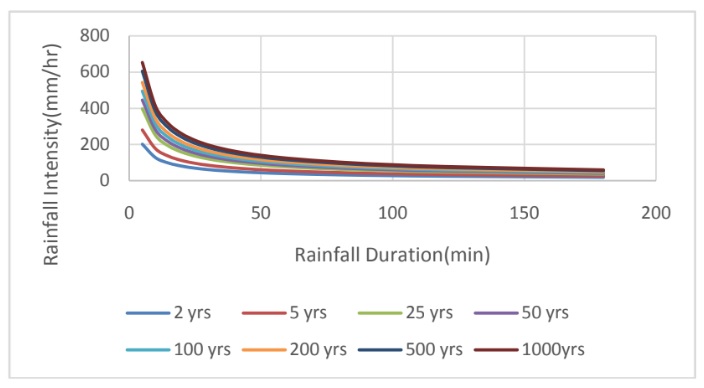
चित्र क्रमांक 1ः जम्मू स्टेशन के लिए तीव्रता की अवधि आवृत्ति वक्र
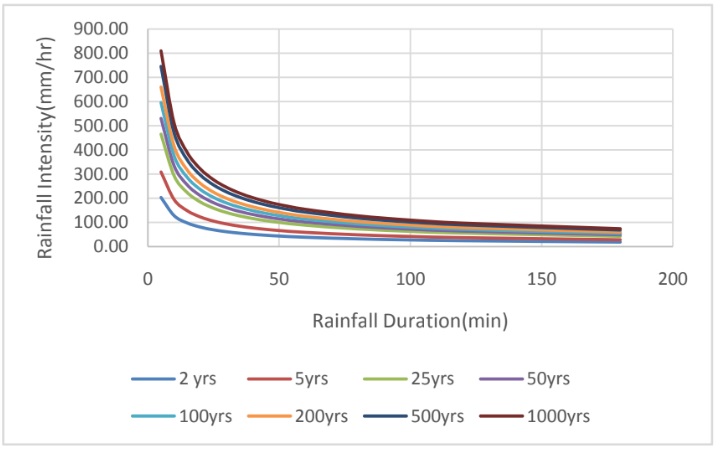
चित्र क्रमांक 2ः बटोट स्टेशन के लिए तीव्रता की अवधि आवृत्ति वक्र
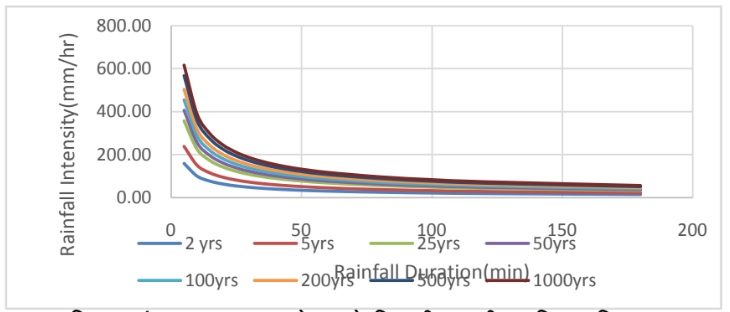
चित्र क्रमांक 3ः भदरवाह स्टेशन के लिए तीव्रता की अवधि आवृत्ति वक्र
4.4 तीव्रता-अवधि-आवृत्ति का अनुभवजन्य संबंध
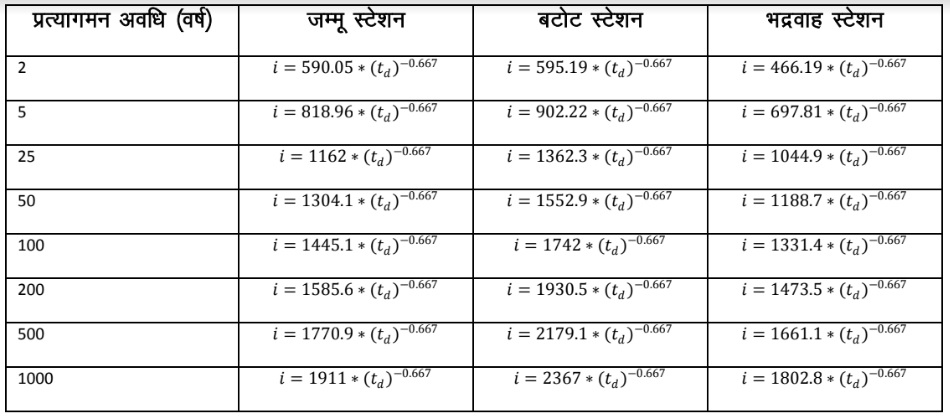
इन आईडीएफ वक्रों का उपयोग थोड़ा सा मुश्किल और लंबा है और इसलिए एक सामान्यीकृत अनुभवजन्य संबंध विकसित किया गया है। आईडीएफ अनुभवजन्य समीकरण के स्थिरांक x और y की गणना अलग-अलग रिटर्न अवधि के लिए की गई । आईडीएफ अनुभवजन्य समीकरण के स्थिरांक x और y को सूत्र 5 के रूप में नीचे दी हुई तालिका क्रमांक 9 में दिखाया गया है।
तालिका 9ःजम्मू स्टेशन के लिए संबंधित वापसी अवधि के लिए वर्षा आईडीएफ अनुभवजन्य समीकरण
 5.0 निष्कर्ष
5.0 निष्कर्ष
इस अध्ययन में, जम्मू कश्मीर में स्थित तवी नदी बसीं के तीन स्टेशनों के लिए अधिकतम वार्षिक वर्षा मानों का उपयोग करके अलग-अलग अवधि के लिए वर्षा की तीव्रता को एक अनुभवजन्य सूत्र द्वारा आकलित किया गया। तत्पश्चात इस डेटा का उपयोग विभिन्न प्रत्यागमन की अवधियों के लिए तीव्रता-अवधि-आवृती वक्रों का निर्माण किया गया। ये वक्र बाढ़ नियंत्रण संरचनाओं के डिजाइन के लिए अधिकतम प्रवाह के आकलन में मदद करते हैं। वर्षा की तीव्रता-अवधि-आवृती वक्र से प्राप्त आंकड़ों की आवश्यकता जल संसाधन और जल संसाधन परियोजनाओं के नियोजन और डिजाइन के लिए इंजीनियरों और जलविज्ञानिकों को होती है। किसी भी प्रत्यागमन की अवधि के लिए किसी भी तूफान की अधिकतम वर्षा की तीव्रता, तीव्रता-अवधि-आवृती (आईडीएफ) वक्र से प्राप्त की जा सकती है। अंत में तवी तीनों स्टेशनों जम्मू, बटोट और भद्रवाह के लिए एक सरल और सामान्यीकृत अनुभवजन्य संबंध विकसित किया गया, जो जलविज्ञानिकों और क्षेत्र के जल अभियंताओं द्वारा उपयोग किया जा सकता है।
Refrence
• Awadallah, A.G., ElGamal, M., ElMostafa, A., ElBadry, H. (2011). Developing intensity–frequency curves in scarce data region: an approach using regional analysis and satellite data. Scientific Research Publishing] Engineering 3, 215–226.
• Chow] V.T (1988). Handbook of Applied Hydrology, McGraw&Hill book
• Chow V.T., D.R.Maidmet and L-W-Mays (1988). “Applied Hydrology”, McGraw& Hill, New York- Probability, Risk and Uncertainty Analysis for Hydrologic and Hydraulic Design,10: 361 – 398-
• Chow V-T- (1964)- Handbook of Applied Hydrology- McGraw & Hill, New York- 9&49, 9&62-
• Kothyari, U.C. and Grade, R.J. (1992) “Rainfall intensity duration frequency formula for India- Journal of Hydraulic Engineering- ASCE, 118 (2), 323&336
• L. Cheng and A.Aghakouchak (2014) Non-stationary precipitation Intensity&Duration&Frequency (IDF) curves for infrastructure design in a changing climate. Scientific Reports.
• Liew, San Chuin, Srivatsan V Raghavan, and Shie.Yui Liong. 2014. “How to Construct Future IDF Curves, under Changing Climate, for Sites with Scarce Rainfall Records?” Hydrological processes 28(8): 3276–87.
• M.M.Rashid, S.B.Faruque and J.B.Alam (2012) Modeling of Short Duration Rainfall Intensity Duration Frequency (SDR.IDF) Equation for Sylhet City in Bangladesh. ARPN Journal of Science and Technology, vol. (2), March.
• Paixao, Edson et al. 2015. “An Integrated Approach for Identifying Homogeneous Regions of Extreme Rainfall Events and Estimating IDF Curves in Southern Ontario, Canada: Incorporating Radar Observations.” Journal of Hydrology 528: 734–50.
• Sane, Youssouph et al. 2018. “Intensity--Duration--Frequency (IDF) Rainfall Curves in Senegal.” Natural Hazards and Earth System Sciences 18(7): 1849–66.
• Singh.V and Zhang.L (2007). Intensity-Duration-Frequency (IDF) curves using the Frank Archimedean Copula. Journal of Hydrologic EngineeringVol.12:651.662, November.
• Singh, Ronit, D S Arya, A K Taxak, and Z Vojinovic. 2016. “Potential Impact of Climate Change on Rainfall Intensity.Duration.Frequency Curves in Roorkee, India.” Water resources management 30(13): 4603–16.
• Yan, Hongxiang et al. 2018. “Next.Generation IDF Curves for Hydrologic Design.” In AGU Fall Meeting Abstracts,.
/articles/daainaika-varasaa-kae-ankadaon-davaaraa-tavai-nadai-baesaina-kae-laie-alaga-alaga